Optimization: constant folding
Today we’re going to talk about about the role of optimization in compilers. We’ll also see how to extend our class compiler with a particular optimization, constant folding.
Optimization: the preliminaries
Let’s start by talking a bit about optimization in general, and then we’ll dive in on implementation.
Why do we call it this?
First let’s talk about this name, optimization. I’ll indulge in a brief rant about this name. It’s rather misleading. When we do “optimization” in the compiler, we’re trying to make programs better. What we’re not doing (or even defining) is making them optimal. So it doesn’t make a ton of sense to say optimizing.
Now, there are variants that do actually optimize, for some definition of optimal. They had to invent a new term for that, superoptimization. In superoptimization, we define a space of possible programs and search for the best program in that space, for some definition of best. For instance, we might decide that we’re searching all sequences of instructions up to length 5 that perform the same task as the 10 instructions we’re optimizing. And then if we have a cost metric, we can pick the sequence of 5 instructions that’s best according to that cost metric.
All of which to say, optimization isn’t a particularly sensible name. But it’s the standard name that we use for these techniques in the field, so we’ll go ahead and call it optimization anyway. We’ll even try not to be too upset about it.
What are we doing? If we’re not making things optimal?
Well, we’re trying to make them better. Here’s our list of criteria, for making a successful optimizer:
- Preserve the meaning of the program.
- Make the program “better”
Q: What do you think we mean by better?
Here are a few things we might mean:
-
runs faster
- runs in less time on my computer
- better worst-case asymptotic execution time
- (note: these two items above are really different)
-
lower memory consumption
- measured
- or worst-case asymptotic
- (same pattern as above)
-
lower energy consumption
- (note: the CPU is the big energy consumer, so people often use run time as proxy)
- small program size
-
no redundant work
- (relates to the faster idea)
-
more effective use of the hardware
- (e.g., better cache utilization)
Here are some other things that we probably think make programs better, but which optimizers aren’t well placed to tackle:
-
readability
- (by the time we’re doing optimization, we’re about to produce assembly, and humans probably aren’t looking at it much anymore!)
-
correctness
- (we already decided the optimizer had to preserve the meaning of the program; it would be frustrating if our compiler was changing our programs’ meanings!)
In lecture, we take some time to talk about each of these and how often we’re ending up doing them. For instance, most of the time—with some exceptions—we’re not changing the worst-case asymptotic execution time of input programs in the optimizer. If you try plotting the runtime of a given program with different input sizes for a well-optimized compiler vs. an unoptimized compiler—or even C++ vs. Python—you’ll see a difference in performance, but it will probably be a constant factor. Most compilers aren’t doing algorithmic changes that alter how the program works. It’s not that it’s not possible! Some transformations do actually change the big O analysis. But it’s safe to assume that the common performance-focused goal, for most optimizers at the moment, is to improve performance by a constant factor, in order to improve execution time on some set of computers that we care about.
Small program size also deserves a bit of a discussion. If we see a 10-line program and a million-line program that do the same thing, we often prefer the short one. In part, we use it as a proxy for performance, but we also just like small programs for their own sake. They’re easier to keep around, easier to move. We do care about this, at least a little, in our compiler. If it’s a choice between a 10-line and a million-line program, and the run time of the million-line program is 10% faster, we’ll probably still want to go with producing the 10-line program. But if it’s a choice between a 10-line program and a 20-line program, and the 20-line program executes 10% faster, we may be willing to take the longer program. We can often do some amount of trading off program size for speed.
We’ll mostly focus on making programs faster rather than on the other goals you may have brainstormed, but we can use some of the same techniques for the other goals.
Where does optimization happen?
Let’s take a moment to zoom out and think about how our whole compiler is structured.
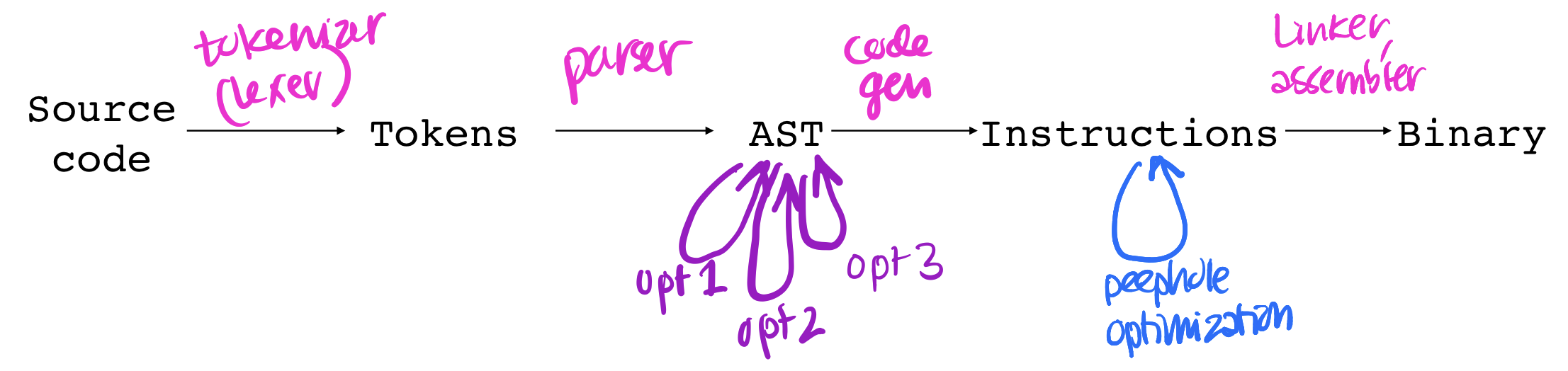
We have the input program string. The tokenizer (or lexer) tokenizes it into tokens. The parser parses the tokens into an AST. The code generator generates assembly from the AST. And the linker (and assembler) produce machine code from the assembly. This process takes us all the way from source code to machine code. It doesn’t look like we need an optimizer along the way. And we don’t! But we can add some if we want.
There are a couple places where we can add them. It’s very common to add optimizers once we have ASTs, and we can use them to transform from one AST to an equivalent AST that will produce more efficient assembly. This is the style of optimizer we’ll see today.
We can also do peephole optimization, which works not on ASTs but on assembly. See lecture capture for a quick example of how peephole optimization works.
What about ordering?
You may notice from the diagram above that we can have multiple optimizations, all of which transform from AST to AST. This may make you wonder—how do we know how to order them? This is an especially big question for industrial compilers which have a lot of these optimization passes, often hundreds and hundreds of them. And the order really matters! It could be that optimization A will find only 3 places to improve if we run it alone, but 300 if we run it after optimization B. So how do we know how to order our optimization passes? Well the short answer is, we don’t.
Deciding how to order optimizations in a compiler is a classic problem called the phase-ordering problem. And basically it’s still a big open question how we should do this. In fact, it’s even more complicated than just picking one slot for each of x optimizations. Sometimes we run optimization A and find 100 places where we can improve things, then run optimization B which changes the AST, and then if we run optimization A again we’ll find another 100 places where we can improve things! So since we don’t have a clean, theoretical framework for how to order these optimizations, what do production compilers do? Essentially, run these optimizations over and over again. Keep circling back around, hoping to find more places to improve everything.
Constant folding
Enough of this chit chat! Let’s implement some stuff.
Here’s our problem: programmers are doing good programming
practices and making their programs readable by doing extra
computation. For instance, say we know a time limit in our program
should be 5 minutes, but our program needs it in milliseconds. Maybe
we write
(let ((time-limit (* 5 (* seconds-per-minute
milliseconds-per-second)))) in ...)
even though we know time-limit will always turn out to
be 300000. We want to let the programmer do that, but we still want
to give them the blazing fast program execution experience of having
written (let ((time-limit 300000)) in ...). And we can
give that to them, via the power of constant folding.
Constant folding is when we recognize that a given expression is a
constant, we go ahead and evaluate the expression to find the
constant, then replace the expression with the constant—all
at compile time.
Here’s a simple program we might want to speed up:
(add1 5)
What program would we like to produce instead? Probably just
6.
So let’s write the transformation that would handle exactly
this case. We’ll write it in a separate
constant_folding.ml file, and then we’ll call it
from the compiler before we start emitting assembly.
let rec fold : expr -> expr = function
| Prim1 (Add1, Num n) ->
Num (n + 1)
| e ->
e
Looks good! With this, we can successfully tackle
(add1 5).
This means we’ve successfully built an optimization! We fulfilled criteria (1) preserves meaning and (2) improves some programs.
But what about this program? (add1 (add1 5)) This time
we’ll try to match with the Prim1 case, but since
(add1 5) is an expr, not a Num, we’ll give up and
send back our original program, (add1 (add1 5)).
Fortunately we can do better:
let rec fold : expr -> expr = function
| Prim1 (Add1, e) -> (
let e = fold e in
match e with Num n -> Num (n + 1) | _ -> Prim1 (Add1, e) )
| e ->
e
Now we make a recursive call to fold once we’ve
matched the outer Add1, so if we find we can reduce the
argument to a Num, we’ll be able to reduce the
outer Add1 as well. That’s exactly what happens
with (add1 (add1 5)). We match the outer
Add1, make a recursive call on the inner
Add1, reduce that to Num 6, and then we
can reduce the outer Add1 to Num 7.
Lovely.
But of course we’re not done. What about
(sub1 (add1 5))? And what about
(let ((x (add1 (add1 5)))) x)?
Here’s the implementation of constant folding once we’ve
gone ahead and traversed more of the AST to catch cases like
(let ((x (add1 (add1 5)))) x). We’ve also added
support for finding constants that are constructed with
Sub1 and Plus. We didn’t bother to
flesh out quite everything. (E.g. there’s no case for
Sub.) But this should give you enough context that you
could complete this compiler pass on your own.
let rec fold : expr -> expr = function
| Num n ->
Num n
| Prim1 (Add1, e) -> (
let e = fold e in
match e with Num n -> Num (n + 1) | _ -> Prim1 (Add1, e) )
| Prim1 (Sub1, e) -> (
let e = fold e in
match e with Num n -> Num (n - 1) | _ -> Prim1 (Sub1, e) )
| Prim1 (p, e) ->
Prim1 (p, fold e)
| If (e1, e2, e3) ->
If (fold e1, fold e2, fold e3)
| Prim2 (Plus, e1, e2) -> (
let e1 = fold e1 in
let e2 = fold e2 in
match (e1, e2) with
| Num x, Num y ->
Num (x + y)
| _ ->
Prim2 (Plus, e1, e2) )
| Prim2 (p, e1, e2) ->
Prim2 (p, fold e1, fold e2)
| Let (v, e, b) ->
Let (v, fold e, fold b)
| e ->
e
let fold_program (prog : program) =
{ body= fold prog.body
; defns=
List.map
(fun {name; args; body} -> {name; args; body= fold body})
prog.defns }
And we can add this optimization pass to our compiler by adding the
call to fold_program:
let compile (program : s_exp list) : string = let prog = program_of_s_exps program in let prog = Constant_folding.fold_program prog in [ Global "entry" ; Extern "error" ; Extern "read_num" ; Extern "print_value" ; Extern "print_newline" ; Label "entry" ] @ compile_exp prog.defns Symtab.empty (-8) prog.body true @ [Ret] @ (List.map (compile_defn prog.defns) prog.defns |> List.concat) |> List.map string_of_directive |> String.concat "\n"
We can tell that our optimization is working:
> compile_and_run "(print (+ 2 (+ 3 (- 5 4))))"
Take a look at the assembly for this program!
Our constant folding implementation above just tackles numbers, but we could do the same thing with Booleans if we wanted!
Discussion
Some reflection questions:
Q: What’s the relationship between constant folding and interpretation?
Q: What AST will we produce for
(sub1 (add1 (add1 (read-num)))) ?
Q: Are we willing to trade off more time spent on compilation for less time spent running the compiled program?
Where can I learn more?
Optimization is a huge, huge area. If you take a grad compilers course, solid chance you’ll spend almost the entire course on optimization, and you still won’t have learned all there is to know. Optimization is still an extremely active area of research, and there’s more happening in this area all the time.
What we’ll be learning in this class are some of the general patterns, which will serve as a solid foundation if you want to learn more optimization techniques going forward. Although we won’t be implementing any additional optimizations in our in-class compiler, we will be seeing more in lecture, so swing by class. And we’ll also be implementing some optimizations in the final homework of the semester.